Accelerometer Primer

Introduction

An accelerometer is a device that is used to measure acceleration in a given axis. Often, several accelerometers are combined to create multi axis accelerometers. The accelerometers that Phidgets sells are 3 axis accelerometers capable of measuring acceleration in all 3 spatial axes. Typically accelerometers report their measurements in terms of g-force or g's which represents the acceleration in increments of earth's standard gravitational acceleration (9.81 m/s²). A stationary object experiences 1g of acceleration due to the earth's gravitational field. For reference, a high speed roller coaster typically develops 4-5g while instantaneous (short duration) g-forces in a car crash can be as high as 100g.

Accelerometers could be used to:

• Detecting the presence of motion and taking basic quantitative measurements.

For example, detecting if a bus is moving, and how aggressively the driver is driving.

• Inertial navigation - estimating speed and position from acceleration.
• Measuring a repetitive motion or vibration over a long period of time.

For example, finding the vibration modes of a large building.

• Measuring tilt.

(In a dynamic system which is moving around, this requires tracking rotation with gyroscopes and/or compasses.)

(In a static system, you only require an accelerometer- preferably one with high resolution and low noise.)

Gravity vs. Acceleration

It's very important to understand the acceleration that Accelerometers measure.

Visualize you are floating weightless in a spaceship in deep space. An accelerometer will show no acceleration (0 g). You strap into your seat, and the rockets fire, accelerating the spaceship (and you) at 9.8 m/s^2 (1 g). The accelerometer will show 1 g of acceleration. The acceleration creates the physical impression of weight / gravity. Accelerometers cannot distinguish between the feeling of weight that you feel when you are accelerated (your speed changes), and the steady pull of gravity.

Stated in a different way - Accelerometers do not measure acceleration due to changes in velocity. Rather, they experience Proper Acceleration - the phenomenon of weight experienced by a test mass that resides in the accelerometer device. On earth, if the accelerometer is sitting on a surface, completely immobile, it will register a non-zero acceleration (gravity). If the device is in free fall it will measure no acceleration.

An accelerometer at rest relative to the Earth's surface will indicate approximately 1 g upwards (Because in order to remain at rest, it is experiencing a force opposite to the earth's gravity- this is called the normal force). To obtain the acceleration due to motion with respect to the Earth, this "gravity offset" must be subtracted. The effects of this acceleration are indistinguishable from any other acceleration experienced by the instrument, so an accelerometer cannot detect the difference between sitting in a rocket on the launch pad, and being in the same rocket in deep space while it uses its engines to accelerate at 1 g. For similar reasons, an accelerometer will read zero during any type of free fall in a vacuum. When free falling through air, the air resistance produces drag forces that reduce the acceleration, until constant terminal velocity is reached. At terminal velocity the accelerometer will indicate 1 g acceleration upwards. For the same reason a skydiver, upon reaching terminal velocity, does not feel as though he or she were in "free-fall", but rather experiences a feeling similar to being supported (at 1 g) on a "bed" of uprushing air.

In order to correct for gravity you will need to determine the tilt angle and subtract 1g in that axis. This means that if you want to measure dynamic acceleration, you can only be sure that you'll be able to measure 1g less than your accelerometer's rated range, since gravity can contribute up to 1g to the measurement and cause the accelerometer to reach its saturation value at a lower acceleration. When the accelerometer saturates, an error will be generated in your program telling you that the value is out of range. For some applications this isn't a big deal, for instance in a remotely controlled vehicle whose accelerometer saturates at a value that can only be reached when the vehicle crashes.

Orientation

Positive and negative directions on all axes for the 1043 - PhidgetSpatial 0/0/3.
Full-size Image

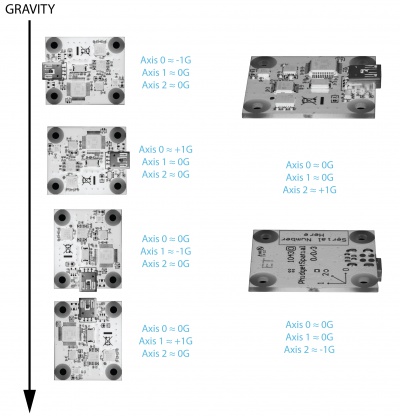
When working with an accelerometer it is important to know which is the +/- direction on each of the axes. This can be determined by orienting the accelerometer along each axis and checking the output. For example, in the image on the right we can see the orientation for the 1043 - PhidgetSpatial 0/0/3 accelerometer. Since the measurement limit is given on a per-axis basis, you could theoretically measure more than the maximum acceleration per axis if the accelerometer was tilted and held in place so that the acceleration being measured is aligned half way between two axes.

Noise

Accelerometer chips will always be effected by some amount of noise, usually caused by thermal and mechanical fluctuations inside the sensor. Noise levels will be different for each axis, because each orientation of sensor is build slightly differently (for example, it is much more difficult to get low noise from the vertical axis because the sensor is a flat piece of silicon. Two of the major types of noise are white noise and random walk.

White Noise

White noise is the short-term noise that is contributed to from a number of internal and external factors. For example, when an accelerometer is stationary on your desk, it might read 1.00g one sample, 0.99g another sample, and 1.02g in yet another sample. Luckily, white noise is usually fairly consistent which means it can be mitigated quite effectively if you average multiple samples together. With a Phidgets Inc. accelerometer, if you select a data rate slower than its maximum it will automatically average as many samples as it can within that time frame for each value. In applications where you need an extremely fast sampling rate, and can't afford to spend time averaging samples, you should look for an accelerometer with low white noise. Also keep in mind the noisiness of your environment- For example, the engine and road noise on a bus will easily be more noisy than the accelerometer - so there is no point in paying for a low noise accelerometer. See the Allan Deviation Primer for more information on accelerometer noise characteristics.

Random Walk

Often called drift, random walk is the long-term noise that causes samples to gradually become further and further away from their true values. This type of noise is less important for applications with constant movement and a fast sampling rate, but for applications where values are averaged over longer periods of time, it can cause severe inaccuracies. See the Allan Deviation Primer for more information on accelerometer noise characteristics.

Accuracy

The rotation platform we use to calibrate our accelerometers and spatial devices. The device being calibrated is secured within the aluminium plates at the top, and the platform rotates on all three axes.
Full-size Image

Accuracy is how close the measured value is to the actual physical property being measured. A sensor with very high resolution and low noise may be returning a very precise (but wrong) answer. When we measure the accuracy of our accelerometers, we average a large number of samples together, which allows us to reduce the effects of short-term noise and get a good idea of how accurate they really are. Accuracy is determined by measuring gravity on the accelerometer (1g) as it is held still in different orientations at room temperature.

Each PhidgetSpatial is individually calibrated. Although this does not remove all errors, the remaining error is non-linear and device specific. If you need higher accuracy, you will only find it in higher end devices, such as aerospace specific accelerometers.

Calculating tilt angle (roll and pitch) from acceleration

One thing people commonly want to determine with an accelerometer is the physical orientation of the object the device is mounted on. This can be done by calculating the tilt angle of the accelerometer board. This is possible due to gravity providing a constant acceleration which can be checked against, meaning we can break the total acceleration down into components and then perform a bit of math to obtain a tilt angle. Tilt angle can only be measured when the accelerometer is stationary. When in motion, the acceleration experienced by the accelerometer is a combination of the device’s physical orientation, and the device’s movement, and the tilt can therefore not be determined. The tilt is calculated as follows-

$Tilt=(arcsin(g_{x}))^{\circ }a_{x}+(arcsin(g_{y}))^{\circ }a_{y}$

Where

$g_{x}$ = acceleration in the x-axis

$g_{y}$ = acceleration in the y-axis

a = indicates which axis the tilt is in

Example of tilt angle calculation-

Axis	Measured Acceleration (g)
x	0.25
y	-0.73

$Tilt=(arcsin(g_{x}))^{\circ }a_{x}+(arcsin(g_{y}))^{\circ }a_{y}$

$Tilt=14.48^{\circ }a_{x}-46.89^{\circ }a_{y}$

When you are looking to use the accelerometer to measure translational acceleration, you will need to calibrate the accelerometer to account for the tilt angle or you will get skewed results.

Calculating Velocity and Position from Acceleration

You can use integrals to estimate velocity from a set of acceleration values. Likewise, if you integrate a set of velocity values, you'll end up with an estimate of the position. Many programming languages have built-in libraries for integration. You'll need to keep track of the data values and the timestamps of each whenever an acceleration change occurs.

High Frequency Vibrations

Harsh vibration will cause the sensor to resonate at very high frequencies - not the frequencies you are trying to measure. This resonance appears on the output as on offset, and is impossible to filter out. The vibration can often be felt - if your application has a metal chassis with motors attached, there is a good chance the chassis will vibrate strongly when the motors are moving. The accelerometer will have to be isolated from the vibration, using vibration mounts. Vibration mounts are simple parts made of rubber, springs, or other elastic materials that can help dampen vibrations to whatever is mounted on them.

Choosing an Accelerometer

The first question to ask when selecting an appropriate accelerometer is "How precise do you need the measurements to be?" Do you just need to sense when an object is moving, with no particular emphasis on the strength of the movement, or do you need accurate data for calculations? You can cut a lost of costs if you only need a basic accelerometer.

Another important criteria is the type of acceleration you're trying to measure. Are they brief, high-acceleration "shocks" of movement, or gradual, moderate acceleration. The answer to this question will determine the type of noise characteristics you're looking for in an accelerometer. The former lends itself to accelerometers with low white noise, since white noise can't be averaged out over many samples if only a few samples reflect the event being measured. The latter is better suited to an accelerometer with low random-walk (also known as drift), since the white noise can be easily averaged out. See the Allan Deviation Primer for more information on noise characteristics.

If you're using the accelerometer to measure high-frequency vibrations, you want to pay attention to the bandwidth of your device. Accelerometers will measure up to a particular frequency of acceleration (easiest to understand as a vibration). Bandwidth specifies the maximum frequency at which the accelerometer will only 'see' 50% of the acceleration. To achieve a particular bandwidth in your application - say you want to measure a vibration or motion with acceleration up to 100Hz, your accelerometer should be rated for at least 150Hz bandwidth (>50% higher), and have a sampling rate of at least 400 samples per second (4x higher).

If you're using the accelerometer as part of a navigation system, you may benefit from adding a gyroscope and compass to aid in calculations. You can keep things simple by getting all three components on one board, such as the 1056 - PhidgetSpatial 3/3/3.